How it works - Halogen

What is Halogen?

For regional planners, Halogen uses local data for more accurate demand prediction, capacity testing, and exploring alternative scenarios.

How is Halogen different?

Models for COVID-19 have varied between statistical time-series analysis (like on the coronavirus dashboard) or extremely complex mathematical models with hundreds of parameters and assumptions (like the nationally used Imperial model). Time-series analysis is accessible to those who are non-mathematically minded (e.g. using Excel and trend lines) however they weren’t made for infectious diseases and so the prediction power is somewhat limited, whereas complex infectious disease mathematical models are extremely sophisticated and require a lot of mathematical knowledge and are often hard to interpret for real-life application, and come with lots of assumptions made about parts of the model which aren’t necessarily transparent or fair to the real-life experience (in favour of being all singing all dancing).

We approached the situation differently - our “mantra” when developing the mathematical model has always been let the data drive the model. Use the available data to build a sophisticated as possible model which minimises assumptions and provides transparency. Then, take the model outputs and communicate the findings in a manner that is accessible to users who can then understand, use, and be confident in describing them.

How does it work?

Upon entering the dashboard, you will see the hospital admissions - both the most up-to-date data you have sent and the resulting fit up to 2 months prior to today's date, and then (assuming a continuation of the current experience) what will happen over the next 4 months if nothing changes - i.e. nothing that would change the nature of the data. Table 1 depicts all the different measurements we demonstrate in the views throughout the dashboard.

We allow you to add some chosen interventions, depicted in Table 2. There are three types of interventions, a type which targets the transmission rate, a type which targets the social mixing and a type which targets both. The transmission rate drives the chance of an infection from a single contacts, whilst the contact mixing determines the average number of contacts (a physical touch or conversation for a certain period of time) a person has per day. A typical intervention that drives the transmission rate up is the introduction of a new variant (this can be modelled by manipulating R). The contacts are typically split into four categories: contacts made at home, contacts made at work, contacts made at school, and other contacts (such as at the park or at the supermarker). A typical intervention that changes the social mixing is closing schools (this can be modelled by removing all school contacts). Once you have chosen which intervention you want to model, you can pick a beginning and end date and then click add intervention. This is then highlighted on the graph. You can add as many interventions as you like, all with different beginning and end dates, which will be reflected on the graph. Once you are happy with what you have modelled, you can export the graph which will give you a csv file of the model outputs and the plot to use for yourself.

You can also change the length of the simulation, the default length is 6 months, 2 months prior to today's date and 4 months afterwards. You can change this to an overall length of 3 months, 1 year, 2 years or 3 years. One should note that, as you increase the overall length, the simulations become less and less accurate.

*: The measurements in Table 1 with an * depict the measurements where data is available and is superimposed on the graph. ⁺: The manipulation of R in Table 2 is done assuming full mixing, that is to say that if you choose R = 1.2 and also the shielding intervention, then the actual value of R will go down since you have removed contacts from the model.

Measurement	Subview	Interpretation
Infectious	Default: Current	Current number of individuals currently infectious
	Cumulative	Cumulative number of individuals infected over the whole epidemic
	New	Daily number of new infectious individuals
Susceptible	Default: Cumulative	Cumulative number of individuals who are still susceptible to COVID-19
Hospital Admissions*	Default: Current	Current number of individuals being admitted into hospital
Hospital Demand*	Default: Current	Current number of patients currently in hospital
Hospital Discharges*	Default: Current	Current number of patients discharged from hospital
Deaths	Default: Cumulative	Cumulative number of individuals who have died over the whole epidemic
Deaths	New*	Daily number of new deaths

[Table 1: Measurements and interpretation]

Intervention	Type	Interpretation
Lockdown	Both	Use the associated transmission rate for the March 2020 Lockdown with the appropriate social mixing
Manipulate R	Transmission	Manipulate the R number⁺
Shielding	Social Mixing	Only household contacts for the elderly population (greater than 70)
School closure (all)	Social Mixing	No contacts for children in primary and secondary schools
School closure (primary)	Social Mixing	No school contacts for children in the primary school age bracket
School closure (secondary)	Social Mixing	No school contacts for children in secondary school age bracket
Working from home	Social Mixing	No work contacts

[Table 2: Interventions]

Can I use it?

We are currently looking for partners but we are approximately 2-3 months away from having fully automated partner areas. If what we offer here at Halogen is something you would like for your region, you can register interest here.

Who made it?

In partnership with Local Authorities (Brighton & Hove City Council, East and West Sussex County Councils) and NHS Sussex Commissioners.

Funding

Higher Education Innovation Fund, University of Sussex.
Brighton & Hove City Council, East and West Sussex County Councils and NHS Sussex Commissioners.

Acknowledgements

Dr. Stephen Wilkins. Email: [email protected].
Pete Goodman. Email: [email protected].

Is it accurate?

For a detailed description of the accuracy of our model, see [1].

In order to test the accuracy of our model and technique, we use a fraction of the data available, calculate the relevant model parameters, and compare the simulated prediction against the remaining data available. We consider that a day is correctly predicted if the data lies within a given number of standard deviations from the simulated prediction. For example, considering the discharge data using a 95% confidence interval, the prediction data is irregular when we use less than 20 data points, but is over 90% accurate using more than 30 data points, even for predictions 30 days into the future! See Figure 3 in [1] for the depiction of this. Moreover, small perturbations in most parameters result in small changes to the over fit of the data, whilst others result in quite a large change in the overall fit (see the supplementary material attached to [1] for this). In this setting, the perturbation of the parameters producing large changes in the overall fit is due to the actual parameters themselves being well characterised from the data rather than the sensitivity of the model.

Note, the accuracy can only be calculated at times when policy (and thus transmission rates) are stable. The model can not predict policy changes and how that changes the transmission rates. In essence, the accuracy of the model is stating that if the outbreak continues exactly as it is (so no policy changing), then using 30 data points we can predict the daily discharges from hospital up to 30 days at a 90% accuracy.

The model

For a detailed description of the SEIR-D model and the mathematics for the inference of the parameters, see [1].

The underlying model is a system of ordinary differential equations describing the flow of people within a population throughout an epidemic, based on a generic SIR model [2]. Each of the equations in the model describes the rate of change of each compartment within the model, with each compartment describing a different characteristic of an individual within the epidemic, as described in Figure 1.

Model Schematic

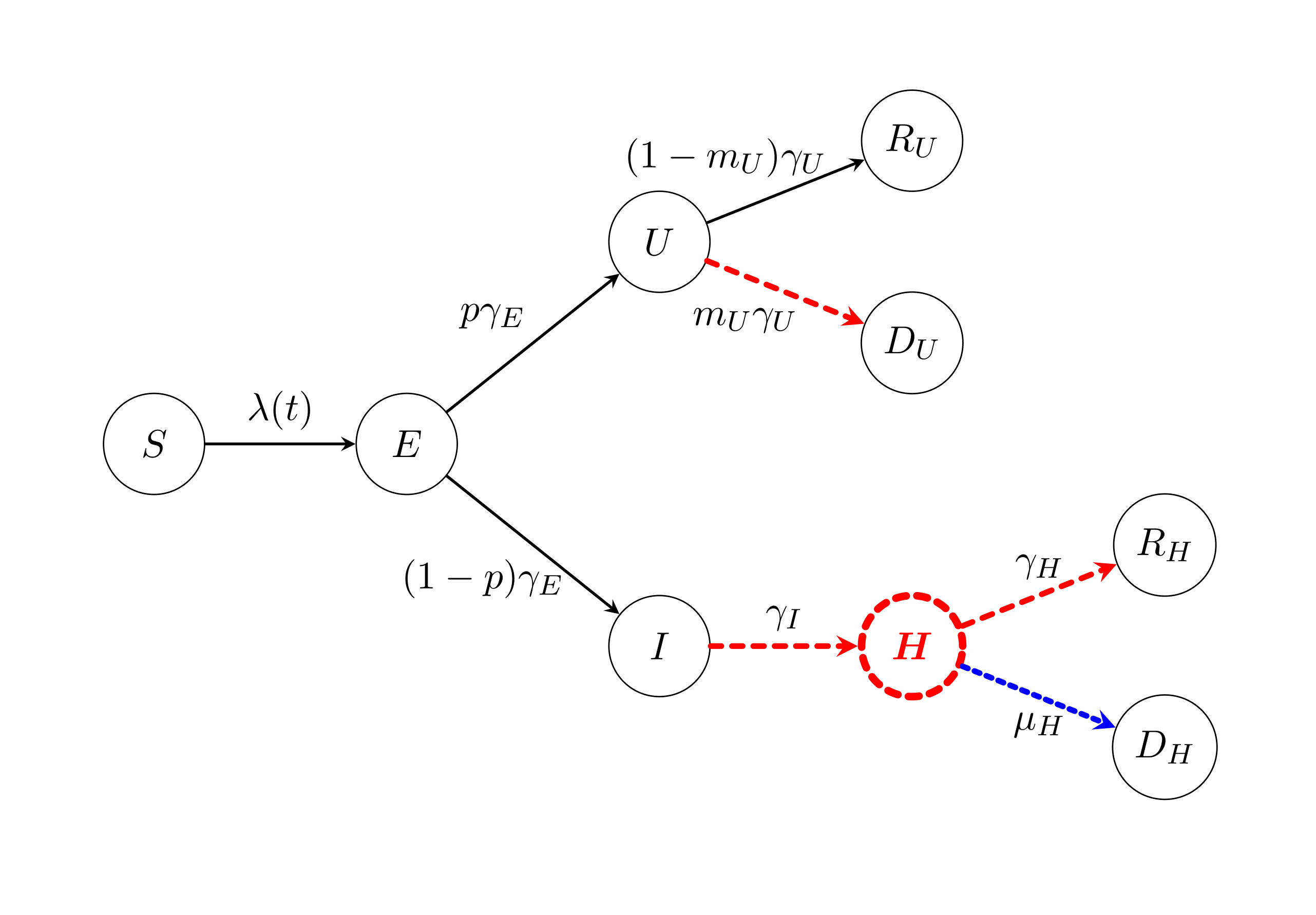
[Figure 1: Schematic representation of the compartmental model]

Each of the circles describes a compartment and each of the arrows describes the rate of which individuals move from one compartment to another. The S(t) compartment describes the susceptible subpopulation, i.e. those who are currently susceptible to COVID-19, whereby one moves from being susceptible to being exposed, E(t), at a rate λ(t). The infection rate λ(t) is made up of the probability of meeting someone who is infectious multiplied to the average transmission rate, denoted β. An individual in the exposed compartment is infected but is not infectious, as it is known that COVID-19 has an incubation period. The traditional infectious compartment is split into two compartments here, those who are infectious and will go to hospital, denoted I(t), and those who are infectious but won't go to hospital, denoted U(t), who therefore (from the point of the view of the hospital) remain undetected by (hospital) testing mechanisms. On average one goes from being exposed to becoming infectious at a rate γ_E and becomes undetected with a probability p or will be going to hospital with a probability 1-p. The undetected compartment is further split into recovered, denoted R_U(t), and died, denoted D_U(t). On average one moves from being infectious at a rate of γ_U and makes a recovery with a probability 1-m_U or dies with a probability of m_U. Upon displaying symptoms, there is often a time between presenting symptoms and actually going to hospital, which is the main difference between the I(t) compartment and the H(t) compartment. An individual is in the H(t) compartment when they are actually in hospital care, and on average one goes from being infectious to being in hospital at a rate γ_I. Once in hospital care, on average one can either recover, denoted R_H(t), at a rate γ_H, or one can die in hospital care, denoted D_H(t), at a rate μ_H. Each of these is parameters and compartments is age-structured in 5-year age-bands. That is to say that for each age-band (there are 18 in total), they have a set of associated parameters and compartments which we aggregate to provide our graphs. Table 3 demonstrates what data we need, the type of data (age-structured or aggregated), the recommended frequency we would like it and the sources our current partners typically find that data. We are aware that the age-structured data is on a lag and take that into consideration in our inference algorithm, same goes for the weekly death registrations.

^x : If you tell us the regions you manage, we can find the ONE 2018 Mid-Year Estimates for your region and import the data in for you.

Data	Type	Frequency	Source
Population Structure	Age-structured	Once upon registration^x	ONS 2018 Mid-Year Estimates
Hospital Admissions	Aggregated	Twice a month	NHS Daily SitReps
Hospital Admissions	Age-structured	Once a month	NHS SUS Hospital Activity
Hospital Cases	Aggregated	Twice a month	NHS Daily SitReps
Hospital Cases	Age-structured	Once a month	NHS SUS Hospital Activity
Hospital Discharges	Aggregated	Twice a month	NHS Daily SitReps
Hospital Discharges	Age-structured	Once a month	NHS SUS Hospital Activity
Hospital COVID-19 Deaths	Aggregated	Twice a month	ONS Death Registrations
Hospital COVID-19 Deaths	Age-structured	Once a month	Civil Registration Data
Care Homes COVID-19 Deaths	Aggregated	Twice a month	ONS Death Registrations
Care Homes COVID-19 Deaths	Age-structured	Once a month	Civil Registration Data
Other COVID-19 Deaths	Aggregated	Twice a month	ONS Death Registrations
Other COVID-19 Deaths	Age-structured	Once a month	Civil Registration Data

[Table 3: Data]

References and further reading

[1] : Campillo-Funollet E, Van Yperen J, Allman P, et al. Predicting and forecasting the impact of local resurgence and outbreaks of COVID-19: Use of SEIR-D quantitative epidemiological modelling for healthcare demand and capacity. medRxiv 2020; published online August 1. DOI: 10.1101/2020.07.29.20164566 (preprint).

[2] : Compartmental models in epidemiology. https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology

[3] : Ferguson NM, Laydon D, Nedjati-Gilani G, et al. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demands. Imperial College, London 2020; published online March 16. DOI: 10.25561/77482.

[4] : Kissler SM, Tedijanto C, Goldstein E, Grad YH, Lipsitch M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 2020; 368:860-8. DOI: 10.1126/science.abb5793.

[5] : Brauer F. Compartmental models in epidemiology. Mathematical epidemiology; 19-79. Heidelberg, Germany: Springer 2008. DOI: 10.1007/978-3-540-78911-6_2.

Coming soon…

Different views of the graphs, such as:
- showing the percentage of total population as the y-axis scale rather than the actual number of people
- scale in comparison to first wave as the y-axis scale, i.e. multiplicatively how much worse is this scenario that the first wave
Including a hospital capacity line for ward capacity planning
Including a mortuary capacity line for death capacity planning
Inclusion of care home data death data
Inclusion of critical care data and an associated views
Including the effect of vaccinations

FAQs

Q: What is the basic reproduction number and how does one calculate it?

A: The basic reproduction number is the expected number of new infections from a single infected individual in a population where all the population is susceptible. Often denoted R₀, one interpretation used is if one person was infected then we would expect R₀ new infections after one day. This number is often used to quantify the infectivity of an outbreak at the beginning of the outbreak.

One calculates R₀ by taking the ratio of the average transmission rate and the average “removal” rate, since R₀ is also interpreted as the average number of contacts an infectious individual makes before they are “removed”. We define removed here in the sense that infectious individuals are not able to be in contact with other individuals.

Q: Is the basic reproduction number and the R number the same?

A:The effective reproduction number, often denoted as the R number or R_t, is the average number of new infections caused by a single infected individual, when considering the proportion of susceptible individuals still remaining to be infected. This is subtly different from R₀ as it depends on the probability of being susceptible as part of the calculation for the infectivity, a value which is more appropriate as an outbreak progresses.

Q: Are you actually predicting the future?

A: We are not predicting the future, we are using modelling scenarios to forecast what could happen depending on the value of R.